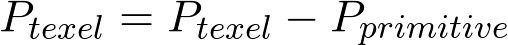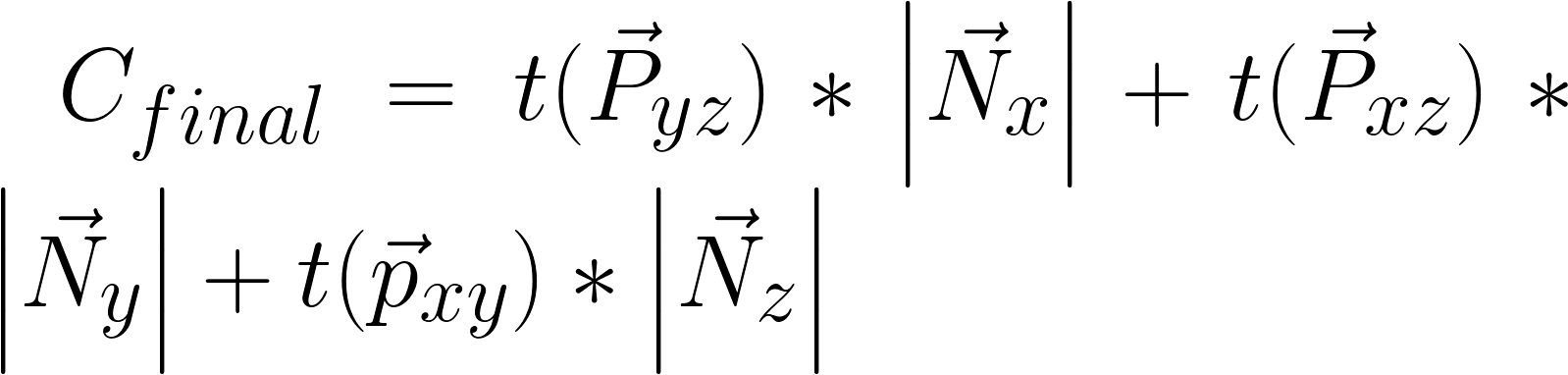Texture sampling

Let's say you have a fragment of geometry in 3D space, with no implicit surface normal or texture coordination, such as one would expect in ray-marching. How does one texture this element in a manner that allows for the texture image to flow over curved geometry? The answer lies in realizing that 3D surfaces exist in any combination of three 2D planes: xy, xz, and yz. Allow me to explain.

First we need to translate our fragment to be of origin from the center of its parent marched primitive, to prevent inconsistencies in primitive positioning.

Where P is either the position of the fragment or the position of the primitive.

This leaves us with a 3D texture coordinate. But wait, we need to use ~2 of them to determine where to sample our texture at! How do we decide which ones to use?

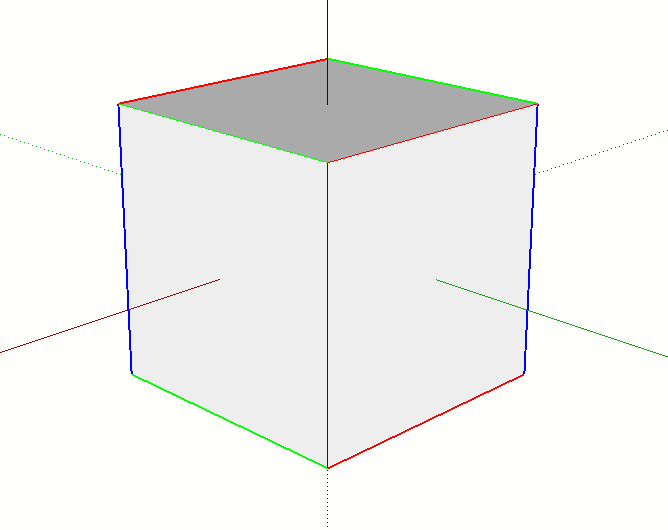
To do this we use the surface normal. The surface normal encodes in which combination of 2D planes the fragment exists in. Allow me to illustrate:

In this image the X axis is red, the Z axis is green, and Y is blue. Just as if it came from Sketchup.

Looking at this diagram it's easy to recognize that if a fragment's normal is entirely in the X direction, its surface exists in the YZ plane, and likewise for the other two axes.

Now that we've seen how a 3D surface exists (as said before) in any combination of the XY, XZ, and YZ planes, it's important that to note that we now sample the 2D texture three times for each fragment--once for each plane--and interpolate them based on the surface's presence in each of the planes. This more than triples the time complexity of texturing operations.

Where C is the final color of the fragment, tex is the texture sampling function, P is the normalized fragment position, and N is the surface normal.

Example code for this technique would look something like this (in GLSL):

/*
  Takes a 3D coordinate, and returns a texel based on which plane(s)
  it lies in.
*/
vec3 tex3D( in vec3 pos, in vec3 normal, in sampler2D sampler )
{
  return texture2D( sampler, pos.yz ).rgb*abs(normal.x)+
    texture2D( sampler, pos.xz ).rgb*abs(normal.y)+
    texture2D( sampler, pos.xy ).rgb*abs(normal.z);
}