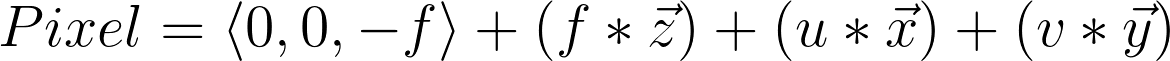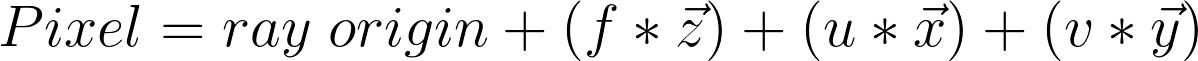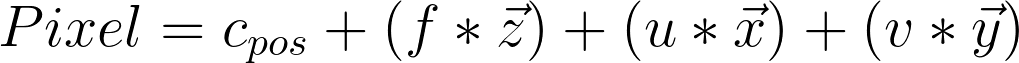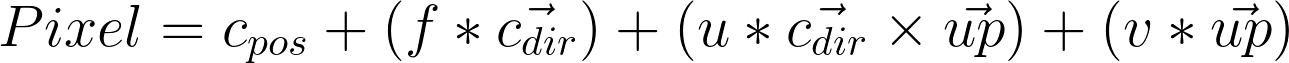A Simple Ray-Marching Camera Function

When I first started ray-marching something I found right away was TekF's polar camera. It's elegant, very good at shooting scenes where the camera need not move, and had a parametrization that, while hefty, made sense.

However, as time went on I started feeling like the TekF solution was a bit too much for my needs; I just wanted a camera function that needs and does as little as possible to give me a ray origin and direction.

The answer I came up with is based around the classic pinhole camera where the ray origin is at some focal distancef behind the screen, and the ray direction is just the pixel's position at the screen (u, v, 0) minus the ray origin, normalized. But let's think: That approach relies heavily on the standard coordinate system; you know, the 3-dimensional space based around x, y and z. Now what if we were to define the origin and direction in such a way that to translate and rotate the camera, we only need to specify our own vectors as the axes of the three dimensions?

In linear algebra, this is essentially a change of basis, with some translation encoded in there too. To start, let's think of what the camera would consider to be its principle axes:

A vector that points up out of the camera would be its Y-axis.
The camera direction--or rather the direction the camera faces-- inherently points along the camera-relative Z-axis.
The cross product of the camera direction and the UP vector would point orthogonally to the right of the camera, becoming an implicit X-axis in the process.

Remember that the original UV coordinates and the distance the focal point is stepped back from the screen are simply multiples of the standard X, Y, and Z basis vectors. Now should we re-imagine our coordinate basis for the camera, if we think of these things in terms of our new basis vectors, we implicitly perform camera translation and orientation.

Recall the ray origin of the standard pinhole camera to be (0, 0, -f), and that the original pixel coordinates were (u, v, 0). A way of thinking about this is:

Where x, y, and z are vectors representing the standard axial directions: (1, 0, 0), (0, 1, 0), and (0, 0, 1).

Now that 3-D coordinate right there is essentially the origin of the camera, so:

Yep kids, that point behind the screen is actually the origin of the vector space the rays exist in.

Really though, being the camera / ray origin makes it the camera position.

Standard basis equation rewritten ... again

Okay, so that really means it's the camera position.

Now let's go ahead and rewrite this equation in terms of our new basis vectors:

Note how x, y, and z have been replaced.

It's as simple as that.To get the ray direction, you simply normalize the subtraction of the ray origin from the pixel position, and the ray origin is simply the camera position.

And with that you have a pinhole camera that you can easily position, in what can be reduced to two lines of GLSL:

/*
  A change-of-basis pinhole camera.
*/
void camera(in vec2 uv, in vec3 cp, in vec3 cd, in float f, out vec3 ro, out vec3 rd)
{
  ro = cp;
  normalize((cp + cd*f + cross(cd, UP)*uv.x + UP*uv.y)-ro);
}