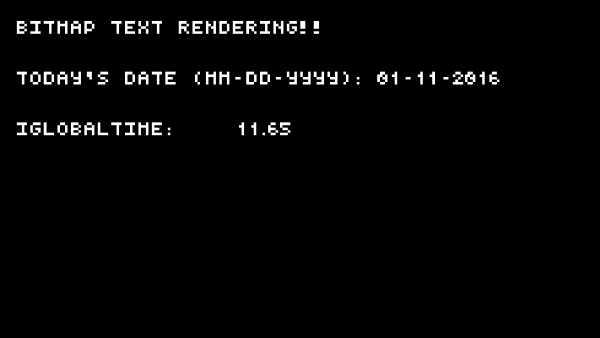
Procedural Bitmap Font Rendering (in a shader)
Constructing and Sampling Glyphs
One of the things that I've always wanted when I've been writing shaders on Shadertoy is text. Apparently I'm not alone in this, too. Many other people have written shaders to produce text entirely within a fragment shader. Perhaps the best example is this shader by P_Malin.
Here he does text two ways: first, by XORing rectangles together to make the characters, and second, encoding 1bpp pixels in floats. The second way is way cooler; cool enough for me to learn it, make some branch-elimating changes, and write about it here.The most important thing to know about this technique is that each glyph is encoded into a float. Let's look at how this is done:
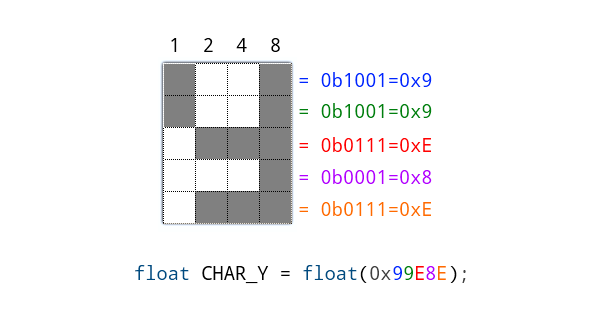
Right up there is a glyph I threw together for the letter 'Y'. Note how it's four pixels wide. (It's also five pixels tall, but that's less important.) This is to allow each row to be stored as a single hexadecimal digit. Then to store the character as a float, you simply have to construct the float with hexidecimal notation, with each digit being a row in the character. The reason we use floats here instead of integers is so that we don't have to typecast every time we want to do some floating point math with these ints.
Now that we've packed these characters, let's discuss how to unpack them to the screen. Not only that, we want to be able to position and resize them.
Generally speaking, we first test to see if the current fragment coordinate is within the character, then we return the value of the bit it lies on. In more detail (since the resizing and positioning adds some complexity):
- Translate the position of the glyph to the origin.
- Scale the fragment coordinate by the size of the glyph, so the dimensions of the glyph become 1x1.
- Do a bounding box check (which is super-simplified, since the box is from (0,0) to (1,1).)
- If the coordinate is within the glyph we multiply it by the bitmap size--in this example(4,5)
- Now by floor()ing the fragment coordinate we have an integer index into the bitmap.
- Sample the bitmap at this coordinate and return the value.
Let's look at this algorithm in GLSL:
Draws a character, given its encoded value, a position, size and
current [0..1] uv coordinate.
*/
float drawChar( in float char, in vec2 pos, in vec2 size, in vec2 uv )
{
// Subtract our position from the current uv so that we can
// know if we're inside the bounding box or not.
uv-=pos;
// Divide the screen space by the size, so our bounding box is 1x1.
uv /= size;
// Bounding box check.
if( min(uv.x,uv.y) < 0.0 && max(uv.x,uv.y) > 1.0 ) return 0.0;
// Go ahead and multiply the UV by the bitmap size so we can work in
// bitmap space coordinates.
uv *= MAP_SIZE;
// Get the appropriate bit and return it.
return getBit( char, 4.0*floor(uv.y) + floor(uv.x) );
}
See? It's pretty straightforward. But this code breaks two gentleman's agreements from the world of GLSL. First is that divide, but there's not much we can do about that within the scope of this function, so it gets to stay. But the second is the branch in the bounding box check.
Sure, with GPGPUs and MIMD architectures becoming ever so commonplace, this isn't too big of a deal anymore. But nevertheless, in a fragment shader branching creates operational overhead like nowhere else. So let's remove it!
Draws a character, given its encoded value, a position, size and
current [0..1] uv coordinate.
*/
float drawChar( in float char, in vec2 pos, in vec2 size, in vec2 uv )
{
// Subtract our position from the current uv so that we can
// know if we're inside the bounding box or not.
uv-=pos;
// Divide the screen space by the size, so our bounding box is 1x1.
uv /= size;
// Create a place to store the result.
float res;
// Branchless bounding box check.
res = step(0.0,min(uv.x,uv.y)) - step(1.0,max(uv.x,uv.y));
// Go ahead and multiply the UV by the bitmap size so we can work in
// bitmap space coordinates.
uv *= MAP_SIZE;
// Get the appropriate bit and return it.
res *= getBit( char, 4.0*floor(uv.y) + floor(uv.x) );
return clamp(res,0.0,1.0); }
The step(min())-step(max()) subtraction will always be zero or less when the UV is outside of the glyph, and one when within. Therefore we can just get the bit (overflow errata will be computed, but never acted upon) and multiply it by the result of the step comparison value. All values outside the bounds of the glyph will be clamped to zero, no branching required.
Converting Values to Characters
So now that we know how to draw glyphs, what if we wanted to display numbers programmatically? What we need is a valToChar() function. Now the first idea you may have for doing this is:
Now we've already talked about this: branching is bad. So let's fix it.
Now this is a bit wonky looking at first, but it uses the same approach as before. Each step comparison will only return 1 if the value is between the edges of the two steps. So as we accumulate each comparison, we will end up only with the character we want.